Mines 2024 - Introduction à 2 problèmes en communication numérique¶
Partie I - Compression du message d'Alice¶
Q1¶
On peut coder 'a' par 0, 'b' par 10 et 'c' par 11 : lorsqu'on lit la chaîne de 0 et 1, si le caractère est 0, alors on a un 'a'. Lorsque ce caractère est '1', alors on regarde le suivant pour savoir s'il vaut 0 ou 1 (et ainsi savoir si on a un 'b' ou un 'c'). Par exemple la chaîne s de l'exemple est codée par
01000100110 (qu'on peut lire 0|10|0|0|10|0|11|0) ; on a donc besoin 11 bits pour la coder ainsi
Analyse du texte source¶
Q2¶
def nbCaracteres(c,s):
total = 0
for car in s:
if car==c:
total +=1
return total
s = 'abaabaca'
nbCaracteres('a',s)
5
Q3¶
def listeCaracteres(s:str):
listeCar = []
n = len(s)
for i in range(n):
c = s[i]
if not(c in listeCar):
listeCar.append(c)
return listeCar
dans la boucle : c désigne le caractère en position i de la chaîne s. On regarde s'il est déjà dans la liste des caractères rencontrés listeCar et si ce n'est pas le cas, on l'ajoute à cette liste. Finalement la fonction renvoie la liste des caractères (uniques) de la chaîne s
On teste sur la chaîne de l'exemple (la fonction va renvoyer la liste ['a','b','c'] :
listeCaracteres(s)
['a', 'b', 'c']
Q4¶
On a $n$ passages dans la boucle. Pour chaque passage, on effectue un test d'appartenance dans une liste qui peut compter jusqu'à $k$ éléments ce qui a une complexité en $O(k)$. Finalement la complexité de la fonction listeCaracteres est $O(nk)$
Éventuellement, il y a une complexité totale en $O(n)$ pour l'affectation de la ligne $5$ et celle du append en ligne $7$ ; cela donne toujours une complexité en $O(nk)$ lorsque $n$ et $k$ sont grands.
Q5¶
On récupère la liste des caractères dans l, ensuite pour chacun des caractères, on ajoute à la liste R un couple sous la forme (caractère, nombre de fois qu'il apparaît dans la chaîne)
def analyseTexte(s:str):
R = []
l = listeCaracteres(s)
for i in range(len(l)):
c = l[i]
R.append((c, nbCaracteres(c, s)))
return R
analyseTexte(s)
[('a', 5), ('b', 2), ('c', 1)]
Q6¶
- on détermine la liste des caractères : complexité en $O(nk)$
- on effectue une boucle avec $k$ passages ; pour chacun de ces passages, on détermine le nombre de caractères correspondants dans la chaîne - cela se fait en une complexité en $O(n)$ (parcourt de la chaîne caractère par caractère) La complexité totale de la boucle est en $O(nk)$
Finalement la complexité asymptotique de analyseTexte est $O(nk)$
Q7¶
def analyseTexteDico(s):
D = {}
for car in s:
if car in D:
D[car] += 1
else:
D[car] = 1
return D
analyseTexteDico("abracadabra")
{'a': 5, 'b': 2, 'r': 2, 'c': 1, 'd': 1}
Le test d'appartenance à un dictionnaire étant (à peu près) en $O(1)$, chaque passage dans la boucle for se fait en temps constants et la fonction complète a une complexité en $O(n)$.
Exploitation d'analyses existantes¶
Q8¶
SELECT DISTINCT auteur FROM corpus
Q9¶
SELECT caractere.symbole, SUM(occurences.nombreOccurences)/SUM(corpus.nombreCaracteres)
FROM corpus
JOIN occurences ON corpus.idLivre=occurences.idLivre
JOIN caractere ON caractere.idCar = occurences.idCar
WHERE langhe ='Français'
GROUP BY caractere.idCar
Quelques explications : on crée la jointure des 3 tables chaque ligne va contenir notamment, le symbole d'un caractère, son nombre d'occurences dans un livre donné et le nombre de caractères total de ce livre. Le GROUP BY sur id.Car va alors faire une partition suivant l'identifiant du caractère. Dans les paquets on aura tous les enregistrements pour chacun des livres avec le nombre d'occureneces de ce caractère et la nombre total de caractères dans chacun des livres.
Remarque : on aurait pu compter le nombre total de caractères avec la requête :
SELECT SUM(nombresCaracteres) FROM corpus WHERE langue = 'Français'
pour l'utiliser dans la requête principale :
SELECT caractere.symbole, SUM(occurences.nombreOccurences)/(SELECT SUM(nombresCaracteres) FROM corpus WHERE langue = ‘Français’)
FROM corpus
JOIN occurences ON corpus.idLivre=occurences.idLivre
JOIN caractere ON caractere.idCar = occurences.idCar
WHERE langhe ='Français'
GROUP BY caractere.idCar
Apparemment le rapport du concours n'accepte pas cela car ils veulent 'UNE' requête (et le SELECT pour calculer le nombre total de caractères compte comme une seconde requête)... personnellement je trouve cela totalement idiot
Compression¶
Q10¶
- le 'b' nous place entre $0.2$ et $0.3$
- dans cet intervalle le 'a' est dans le $20%$ de la longueur $0.1$ donc entre $0.20$ et $0.22$
- enfin le 'c' est entre le $30%$ et le $50%$ de cet intervalle de longueur $0.02$ donc entre $0.206$ et $0.210$ (exclu)
Q11¶
def codage(s):
g,d = 0,1
for c in s:
g,d = codeCar(c,g,d)
return g,d
On effectue un test avec les fréquences de l'exemple (et uniquement les 5 caractères)
def codeCar(c,g,d):
long = d-g
D = {'a': (0,0.2), 'b': (0.2,0.3), 'c': (0.3,0.5), 'd':(0.5,0.9), 'e':(0.9,1)}
g1,g2 = D[c]
return g+g1*long,g+g2*long
codage('dac')
(0.524, 0.54)
codage('bac')
(0.20600000000000002, 0.21000000000000002)
Décodage¶
Q12¶
dans l'intervalle $[0.10,0.18[$ (de longueur $0.08$, les séparations sont (en ajoutant ensuite le point de départ à 0.10) :
$0 - 0.016 - 0.024 - 0.040 - 0.072 - 0.08$
c'est-à-dire
$0.100 | 0.116 | 0.124 | 0.140 | 0.172 | 0.180$
le $0.123$ est dans le second intervalle $[0.116 ; 0.124[$ donc le troisième caractère est un 'b'
Q13¶
Le $0.2$ indique qu'on commence par un 'b'. Le problème est qu'après, un peut ne plus avoir de caractères ou bien dire que cela peut être un 'a' (et en fait même plusieurs 'a'). Cela peut donc coder la chaîne 'b' et la chaîne 'ba' (cela vient du fait que la borne gauche de l'intervalle de 'a' est acceptée)
Q14¶
def decodage(x):
chaine = ''
g,d = 0,1
car = decodeCar(x,g,d)
while car != '#':
chaine = chaine + car
g,d = codeCar(car,g,d) # nouvelle zone gauche/droite
# on peut aussi remplacer par
# g,d = codage(chaine)
# qui renvoie l'intervalle de la chaîne déjà construite
car = decodeCar(x,g,d) # nouveau caractère
return chaine + "#"
Partie II - Décodage du message reçu par Bob¶
Q15¶
On a $N$ colonnes de $K$ sommets donc $K.N$ sommets au total. De chacun des sommets sur les $N-1$ premières colonnes (il y en a donc $K*(N-1)$ partent $K$ arêtes ce qui donne $(N-1)K^2$ arêtes.
Q16¶
l'image n'est pas de moi mais d'un autre corrigé :
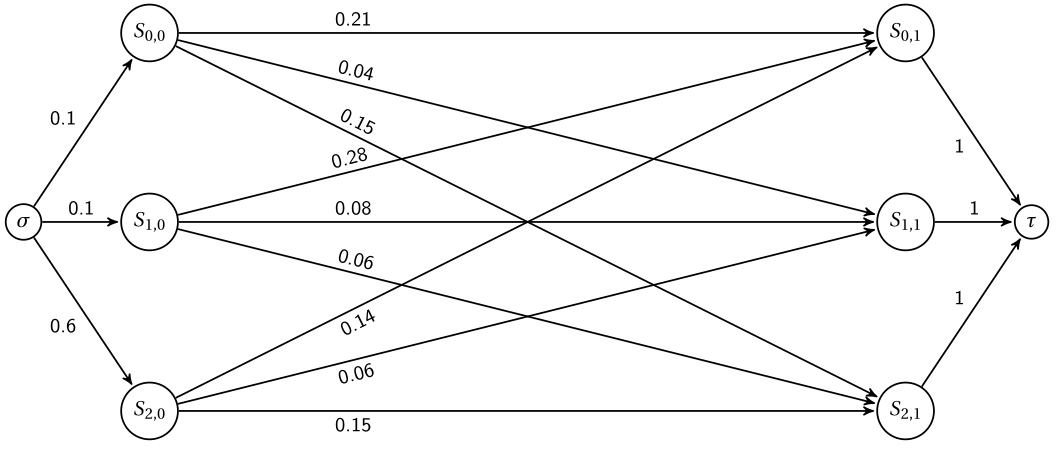
Q17¶
À chaque étape, on a $K$ possibilités. Il y a $N$ étapes et donc $K^N$ chemins... beaucoup trop pour tous les parcourir
Q18¶
def maximumListe(liste):
pos = 0
maxi = liste[0]
for i in range(1,len(liste)):
a = liste[i]
if a>maxi:
maxi = a
pos = i
return maxi,pos
maximumListe([3,5,7,4,3,7,2,3])
(7, 2)
Q19¶
def glouton(Obs, P, E, K):
actuel = initialiserGlouton(Obs,E,K) # lettre actuelle
s = [actuel]
for j in range(1,N):
L = [E[Obs[j]][actuel] * P[i][j] for i in range(K)]
maxi, actuel = maximumListe(L)
s.append(actuel)
return s
Q20¶
- L'initialisation est en $O(N)$
- on effectue une boucle avec $N-1$ passages, chaque passage est en $O(K)$ (un $O(K)$ pour la construction de la liste et un autre pour la recherche de la position du maximum)
Finalement la fonction est en $O(NK)$.
Q21¶
On choisit la première branche à $0.6$. Arrivé à ce sommet, on choisit le 0.5 (puis le $1$). Cela donne un chemin $(0,0)$ de poids $0.3$. On remarque que le chemin $(1,0)$ a un poids de $0.4*0.9=0.36$ est meilleur. L'algorithme glouton n'est donc pas optimal pour ce problème.
Q22¶
Un chemin entre le sommet $\sigma$ et $\tau$ passe exactement par un et un seul sommet de chaque colonne donc correspond exactement à un message que l'on cherche. Le poids d'un chemin et le produit des probabilités. Le logarithme de ce poids total est la somme des logarithmes des poids. Cela revient donc à chercher un plus court chemin (en somme des distances) par rapport à ces nouveaux poids. On peut par exemple utiliser l'algorithme de Dijkstra pour déterminer ce plus court chemin.
Q23¶
On remplit de la gauche vers la droite les deux matrices. Pour chaque case de la colonne $j$, on utilise les formules du haut de la page 11 pour savoir comment remplir T[i][j] et argT[i][j] :
def construireTableauViterbi(Obs, P, E, K, N):
T, argT = initialiserViterbi(E,Obs,K,N)
for j in range(1,N):
for i in range(K):
table = [T[k][j-1] * P[k][i] * E[Obs[j]][i] for k in range(K)]
maxi,pos = maximumListe(table)
T[i][j] = maxi
argT[i][j] = pos
return T,argT
Q24¶
On part de la dernière colonne de $T$ et on cherche quelle est la probabilité maximale. Elle est en ligne $0$ ce qui donne un dernier caractère $0$. En cette position $(0,7)$, la valeur de argT est $0$ ce qui signifie que le maximum a été obtenu à partir de la case $(0,6)$. On refait le même raisonnement à partir de cette case (on a seulement à suivre les cases d'origine) ; on a un caractère $0$ et on vient donc de la case $(1,5)$ (qui donnera un caractère $1$) . Cela donne le chemin inverse
0 -> 0 -> 1 -> 1 -> 2 -> 0 -> 0 -> 2
et ainsi le message $[2,0,0,2,1,1,0,0]$
Q25¶
- Complexité temporelle :
- on commence par initialiser :
- la création des deux listes de listes est en $O(NK)$
- le remplissage de la première colonne en $O(K)$
- on a alors une double boucle avec $NK$ passages. Dans chaque passage, on construit une liste à $K$ éléments et on cherche le maximum et sa position en complexité $O(K)$
- Finalement la complexité temporelle est en $O(NK^2)$ (c'est $K$ fois plus que l'algorithme glouton mais $K$ est le nombre de caractère donc c'est plutôt controlé... on reste linéaire par rapport à la taille du message
- on commence par initialiser :
- Pour la complexité spatiale, on a deux listes de taille $NK$ et on crée à chaque passage une liste de taille $K$ (mais qu'on ne stocke pas plus longtemps qu'un passage de boucle). La complexité spatiale est donc $O(NK)$